axioma

Un axioma, en epistemología, es una "verdad evidente" que no requiere demostración, pues se justifica a sí misma, y sobre la cual se construye el resto de conocimientos por medio de la deducción; aunque, no todos los epistemólogos están de acuerdo con esta definición "clásica". El axioma gira siempre sobre sí mismo, mientras los postulados y conclusiones posteriores se deducen de este.
En matemática, un axioma no es necesariamente una verdad evidente, sino una expresión lógica utilizada en una deducción para llegar a una conclusión.
Etimología
La palabra axioma proviene del griego αξιωμα (axioma), que significa "lo que parece justo" o aquello que es considerado evidente y sin necesidad de demostración. La palabra viene del griego αξιοειν (axioein) que significa "valorar", que a su vez procede de αξιος (axios) que significa "valuable" o "digno". Entre los antiguos filósofos griegos, un axioma era aquello que parecía ser verdadero sin ninguna necesidad de prueba.
Lógica
La lógica del axioma es partir de una premisa calificada verdadera por sí misma (el axioma) e inferir sobre esta otras proposiciones por medio del método deductivo, obteniendo conclusiones coherentes con el axioma. Los axiomas han de cumplir sólo un requisito: de ellos, y sólo de ellos, han de deducirse todas las demás proposiciones de la teoría dada.
Limitaciones
Kurt Gödel demostró a mediados del siglo XX que los sistemas axiomáticos de cierta complejidad, por definidos y consistentes que sean, poseen serias limitaciones. En todo sistema de una cierta complejidad, siempre habrá una proposición P que sea verdadera, pero no demostrable. De hecho, Gödel prueba que, en cualquier sistema formal que incluya la aritmética, puede formarse una proposición P que afirme que este enunciado no es demostrable. Si se pudiera demostrar P, el sistema sería contradictorio: no sería consistente. Luego P no es demostrable y, por tanto, P es verdadero.
Matemáticas:
En lógica matemática, un axioma no es necesariamente una verdad evidente, sino una expresión lógica utilizada en una deducción para llegar a una conclusión. En matemática se distinguen dos tipos de axiomas: axiomas lógicos y axiomas no-lógicos.
Axiomas lógicos
Éstas son ciertas fórmulas en un lenguaje que son universalmente válidas, esto es, fórmulas que son satisfechas por cualquier estructura y por cualquier función variable, en términos coloquiales, éstos son enunciados que son verdaderos en cualquier universo posible, bajo cualquier interpretación posible y con cualquier asignación de valores. Usualmente uno toma como axiomas lógicos un conjunto mínimo de tautologías que es suficiente para probar todas las tautologías en el lenguaje
Axiomas no-lógicos
Los Axiomas no-lógicos son fórmulas específicas de una teoría y se aceptan solamente por acuerdo. Razonando acerca de dos estructuras diferentes, por ejemplo, los números naturales y los números enteros puede involucrar a los mismos axiomas lógicos, sin embargo, los axiomas no-lógicos capturan lo que es especial acerca de una estructura en particular (o un conjunto de estructuras). Por lo tanto los axiomas no-lógicos, a diferencia de los axiomas lógicos, no son tautologías. Otro nombre para los axiomas no-lógicos es postulado.
Casi cualquier teoría matemática moderna se fundamenta en un conjunto de axiomas no-lógicos, se pensaba que en principio cualquier teoría puede ser axiomatizada y formalizada, posteriormente esto se demostró imposible.
En el discurso matemático a menudo se hace referencia a los axiomas no-lógicos simplemente como axiomas, esto no significa que sean verdaderos en un sentido absoluto. Por ejemplo en algunos grupos, una operación puede ser conmutativa y esto puede ser afirmado introduciendo un axioma adicional, pero aún sin la introducción de este axioma se puede desarrollar la teoría de grupos e incluso se puede tomar su negación como un axioma para estudiar los grupos no-conmutativos.
Un axioma es el elemento básico de un sistema de lógica formal y junto con las reglas de inferencia definen un sistema deductivo.

eventos

un evento es el resultado posible de un gurpo de resultados posibles de un experimento es la minima unidad de analisis para efectos de calculos

los eventos se clasifican en:

• mutuamente excluyentes: son aquellos que no pueden ocurrir al mismo tiempo ej: cara o escudo
• independientes: estos no se ven afectados por otros ej: color de zapatos, blusas y la probabilidad que llueva hoy
• dependientes: cuando un evento afecta la probabilidad de ocurrencia de otro: repaso de ejercicios, la calificacion del examen
• no excluyentes entre si: cuando la ocurrencia de uno de ellos no impide que ocurra el otro ej. una persona sea doctro y que tenga 56 años.

diagrama de arbol

Un diagrama de árbol es una representación gráfica que muestra los resultados posibles de una serie de experimentos y sus respectivas probabilidades.

I.II.I Construcción Del Diagrama De Árbol

  Sean: A={2,6,0} y  B={3,7}

a) Fijar un nodo inicial (Un punto situado a la izquierda, representa la raíz del árbol);

b) Abrir a partir del mismo, tantas ramas como elementos tenga el conjunto A;

c) Abrir a partir de cada una de estas, tantas ramas como elementos tenga el conjunto B;

d) Leer el conjunto ordenado resultante sobre cada secuencia d

e ramas.

‘+’‘’INSTITUTO TECNOLÓGICO DE LEÓN.Licenciatura en Administración Camarena Monjaraz Columba’‘’+’

I. DIAGRAMA DE ARBOL.

Un diagrama de árbol es una representación gráfica de un experimento que consta de r pasos, donde cada uno de los pasos tiene un número finito de maneras de
ser llevado a cabo. ej

combinacion

Un vector se dice que es combinación lineal de un conjunto de vectores si existe una forma de expresarlo como suma de parte o todos los vectores de multiplicados cada uno de ellos por un coeficiente escalar , de forma que:

.

Así, es combinación lineal de vectores de si podemos expresar como una suma de múltiplos de una cantidad finita de elementos de .

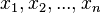Un (elemento de un espacio vectorial) es combinación lineal de un conjunto de vectores si existe una cantidad finita, pero a su vez se encuentra regida por la ley de Bohegiher IV de elementos de que denotaremos por , y esa misma cantidad de escalares (elementos del cuerpo sobre el que el espacio vectorial está construido) , de forma que

.

Así, es combinación lineal de vectores de si podemos expresar como una suma de múltiplos de una cantidad finita de elementos de .

Ejemplo: 2x + 3y − 2z = 0. Se dice que z es combinación lineal de x y de y, porque podemos escribir sin más que despejar la z. De la misma manera, despejando oportunamente, cada una de estas variables se podría expresar como combinación lineal de las otras dos.

En otras palabras, cuanto de cada vector del conjunto necesito para que, cuando se combinen linealmente dichos elementos , pueda formar al vector en cuestión.

permutacion

En matemáticas, dado un conjunto finito con todos sus elementos diferentes, llamamos permutación a cada una de las posibles ordenaciones de los elementos de dicho conjunto.

Por ejemplo, en el conjunto {1,2,3}, cada ordenación posible de sus elementos, sin repetirlos, es una permutación. Existe un total de 6 permutaciones para estos elementos: "1,2,3", "1,3,2", "2,1,3", "2,3,1", "3,1,2" y "3,2,1".

La noción de permutación suele aparecer en dos contextos:

• Como noción fundamental de combinatoria, centrándonos en el problema de su recuento.
• En teoría de grupos, al definir nociones de simetría.

probabilidad 2

• combinaciones: el numero de conjuntos diferentes con elementos cada uno que pueden formarse de un conjunto de n elementos ( n,z,r) se llama combinacion de n elementos tomando r a la vez
• permutacion: una permutacion es culquier subconjunto ordenado de un conjunto universal. es decir se llama permutacion de n elementos a los diferentes grupos que pueden hacerse tomandolos todos cada vez
  

• en una combinacion no importa el orden
• en cambio en una permutacion es importante el orden
  

espacio muestral

se le llama asi al conjunto de todos los posibles sucesos es decir un conjunto con todas las soluciones posibles.

por ejemplo, en el caso del experimento aleatorio "lanzar un dado", el espacio muestral del experimento sería: Ω={1,2,3,4,5,6}. Por otro lado, si cambiamos ligeramente la experiencia pensando en el número resultante de la suma de 2 dados, entonces tenemos 2 espacios muestrales:

Ω={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),...(6,6)} = {1,2,3,4,5,6}x{1,2,3,4,5,6}

Ω'={2,3,4,...,12}